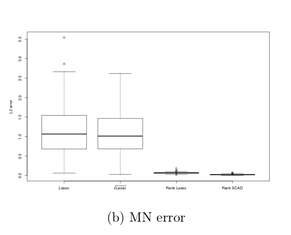
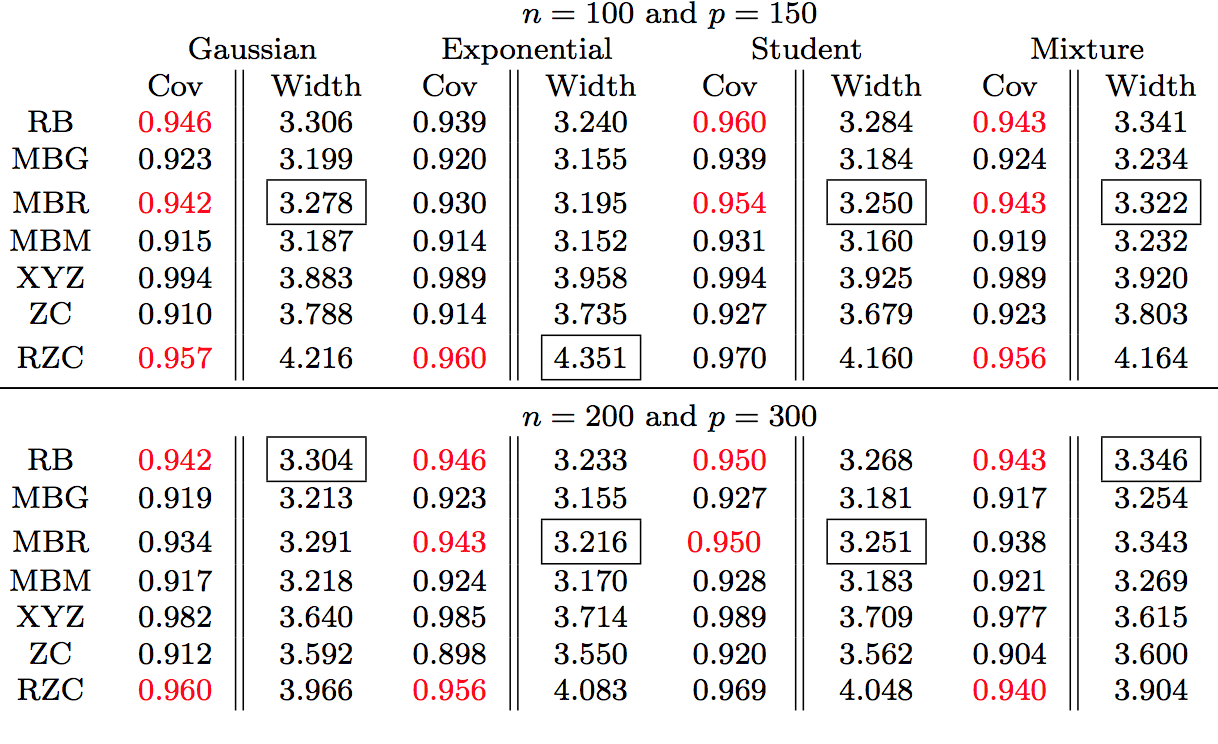
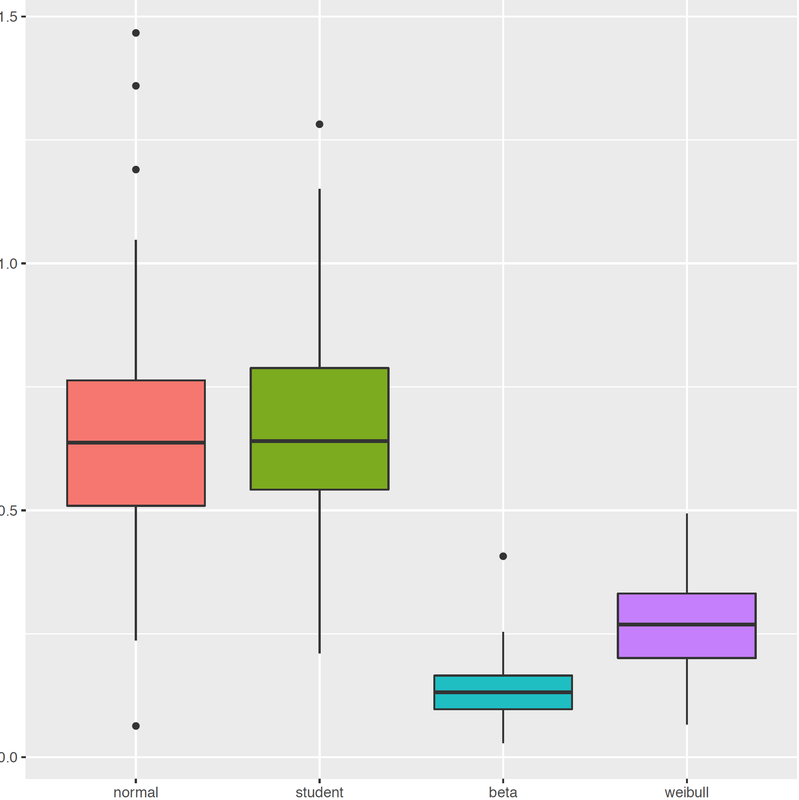
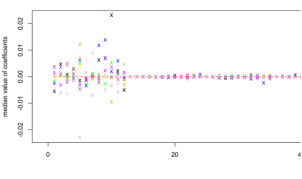
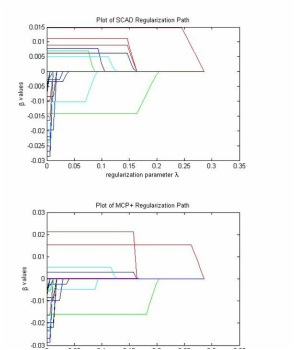
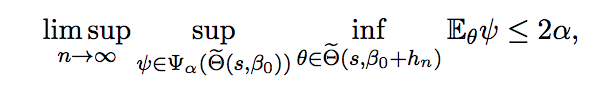A tuning free robust and efficient approach to high-dimensional regression

We introduce a novel approach for high-dimensional regression with theoretical guar- antees. The new procedure overcomes the challenge of tuning parameter selection of Lasso and possesses several appealing properties. It uses an easily simulated tuning parameter that automatically adapts to both the unknown random error distribution and the correlation structure of the design matrix. It is robust with substantial effi- ciency gain for heavy-tailed random errors while maintaining high efficiency for normal random errors. Comparing with other alternative robust regression procedures, it also enjoys the property of being equivariant when the response variable undergoes a scale transformation. Computationally, it can be efficiently solved via linear programming. Theoretically, under weak conditions on the random error distribution, we establish a finite-sample error bound with a near-oracle rate for the new estimator with the sim- ulated tuning parameter. Our results make useful contributions to mending the gap between the practice and theory of Lasso and its variants. We also prove that further improvement in efficiency can be achieved by a second-stage enhancement with some light tuning. Our simulation results demonstrate that the proposed methods often outperform cross-validated Lasso in various settings.

        with Lan Wang, Runze Li, Yunan Wu and Bo Peng
              forthcoming (with discussion) in the 
                         Journal of the American Statistical Association: T&M 

Rejoinder for "A tuning free robust and efficient approach to high-dimensional regression"

We heartily thank the Editors, Professors Regina Liu and Hongyu Zhao, for featuring
this paper and organizing stimulating discussions. We are grateful for the feedback on our work from the three distinguished discussants: Professors Jianqing Fan, Po-Ling Loh and Ali Shaojie. The discussants provide novel methods for inference, offer new applications such as graphical models and factor models, and highlight the possible impact of robust procedures in new domains. Their discussions have pushed forward robust high-dimensional statistics in disparate directions. These in-depth discussions with new contributions would easily qualify on their own as independent papers in the field of robust high-dimensional statistics. We sincerely thank the discussants for their time and effort in providing insightful comments and for their generosity in sharing their new findings. In the following, we organize our rejoinder around the major themes in the discussions.

with Lan Wang, Runze Li, Yunan Wu and Bo Peng
              forthcoming in the 
                         Journal of the American Statistical Association: T&M

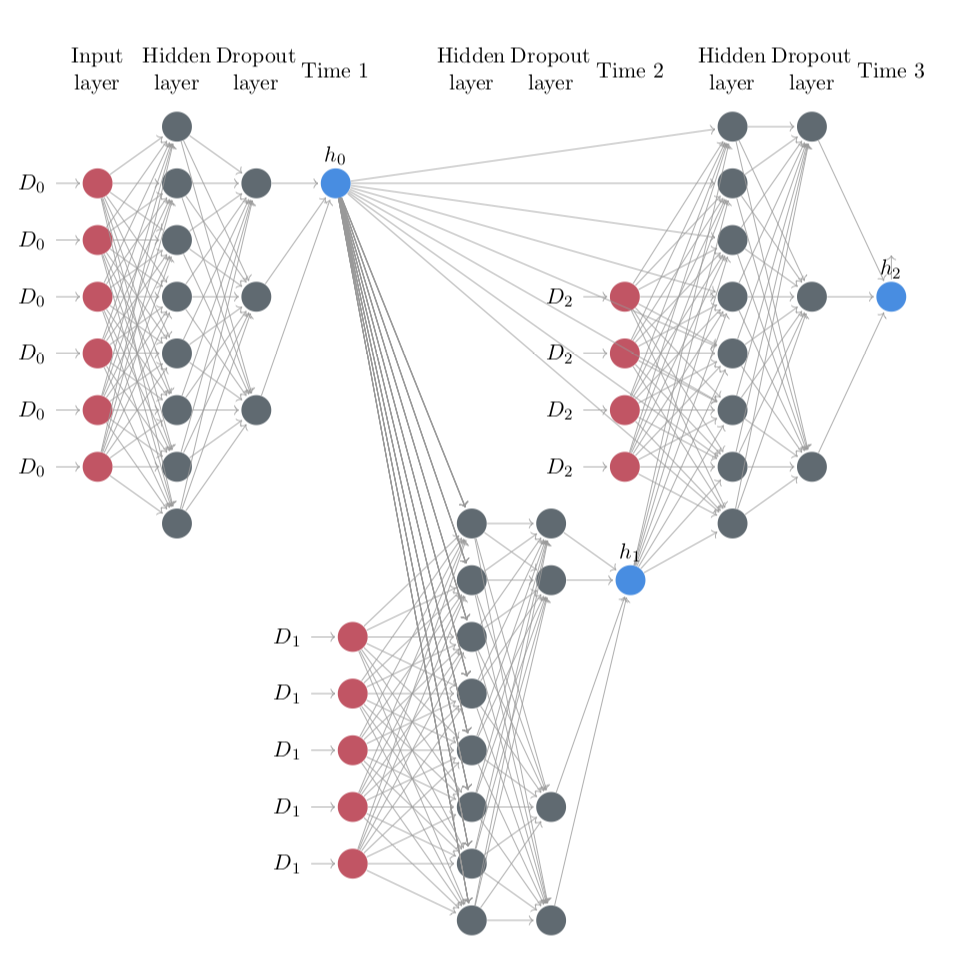
DeepHazard:
​neural network for time-varying risks

Prognostic models in survival analysis are aimed at understanding the relationship between patients' covariates and the distribution of survival time. Traditionally, semi-parametric models, such as the Cox model, have been assumed. These often rely on strong proportionality assumptions of the hazard that might be violated in practice. Moreover, they do not often include covariate information updated over time. We propose a new flexible method for survival prediction: DeepHazard, a neural network for time-varying risks. Our approach is tailored for a wide range of continuous hazards forms, with the only restriction of being additive in time. A flexible implementation, allowing different optimization methods, along with any norm penalty, is developed. Numerical examples illustrate that our approach outperforms existing state-of-the-art methodology in terms of predictive capability evaluated through the C-index metric. The same is revealed on the popular real datasets as METABRIC, GBSG, and ACTG.

        with Denise Rava
​            submitted

Detangling robustness in high dimensions:
​composite versus model-averaged estimation

Robust methods, though ubiquitous in practice, are yet to be fully understood in the context of regularized estimation and high dimensions. Even simple questions become challenging very quickly. For example, classical statistical theory identifies equivalence between model-averaged and composite quantile estimation. However, little to noth- ing is known about such equivalence between methods that encourage sparsity. This paper provides a toolbox to further study robustness in these settings and focuses on prediction. In particular, we study optimally weighted model-averaged as well as com- posite l1-regularized estimation. Optimal weights are determined by minimizing the asymptotic mean squared error. This approach incorporates the effects of regulariza- tion, without the assumption of perfect selection, as is often used in practice. Such weights are then optimal for prediction quality. Through an extensive simulation study, we show that no single method systematically outperforms others. We find, however, that model-averaged and composite quantile estimators often outperform least-squares methods, even in the case of Gaussian model noise. Real data application witnesses the method’s practical use through the reconstruction of compressed audio signals.

        with Gerda Claeskens and Jing Zhou
             Electronic Journal of Statistics (2020), 14 (2), 2551-2599.

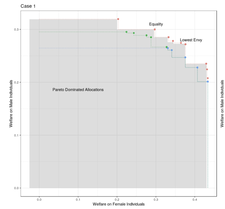
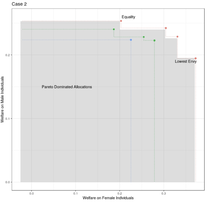
Fair Policy Targeting

One of the major concerns of targeting interventions on individuals in social welfare programs is discrimination: individualized treatments may induce disparities on sensitive attributes such as age, gender, or race. This paper addresses the question of the design of fair and efficient treatment allocation rules. We adopt the non-maleficence perspective of "first do no harm": we propose to select the fairest allocation within the Pareto frontier. We provide envy-freeness justifications to novel counterfactual notions of fairness. We discuss easy-to-implement estimators of the policy function, by casting the optimization into a mixed-integer linear program formulation. We derive regret bounds on the unfairness of the estimated policy function, and small sample guarantees on the Pareto frontier. Finally, we illustrate our method using an application from education economics.

with Davide Viviano
    submitted
​

Minimax Semiparametric Learning With Approximate Sparsity

 Many objects of interest can be expressed as a linear, mean square continuous functional of a least squares projection (regression). Often the regression may be high dimensional, depending on many variables. This paper gives minimal conditions for root-n consistent and efficient estimation of such objects when the regression and the Riesz representer of the functional are approximately sparse and the sum of the absolute value of the coefficients is bounded. The approximately sparse functions we consider are those where an approximation by some t regressors has root mean square error less than or equal to Ct^{-ξ} for C, ξ>0. We show that a necessary condition for efficient estimation is that the sparse approximation rate ξ1 for the regression and the rate ξ2 for the Riesz representer satisfy max{ξ1,ξ2}>1/2. This condition is stronger than the corresponding condition ξ1+ξ2>1/2 for Holder classes of functions. We also show that Lasso based, cross-fit, debiased machine learning estimators are asymptotically efficient under these conditions. In addition we show efficiency of an estimator without cross-fitting when the functional depends on the regressors and the regression sparse approximation rate satisfies ξ1>1/2.

​           with Victor Chernozhukov, Whitney Newey and Yinchu Zhu
                submitted

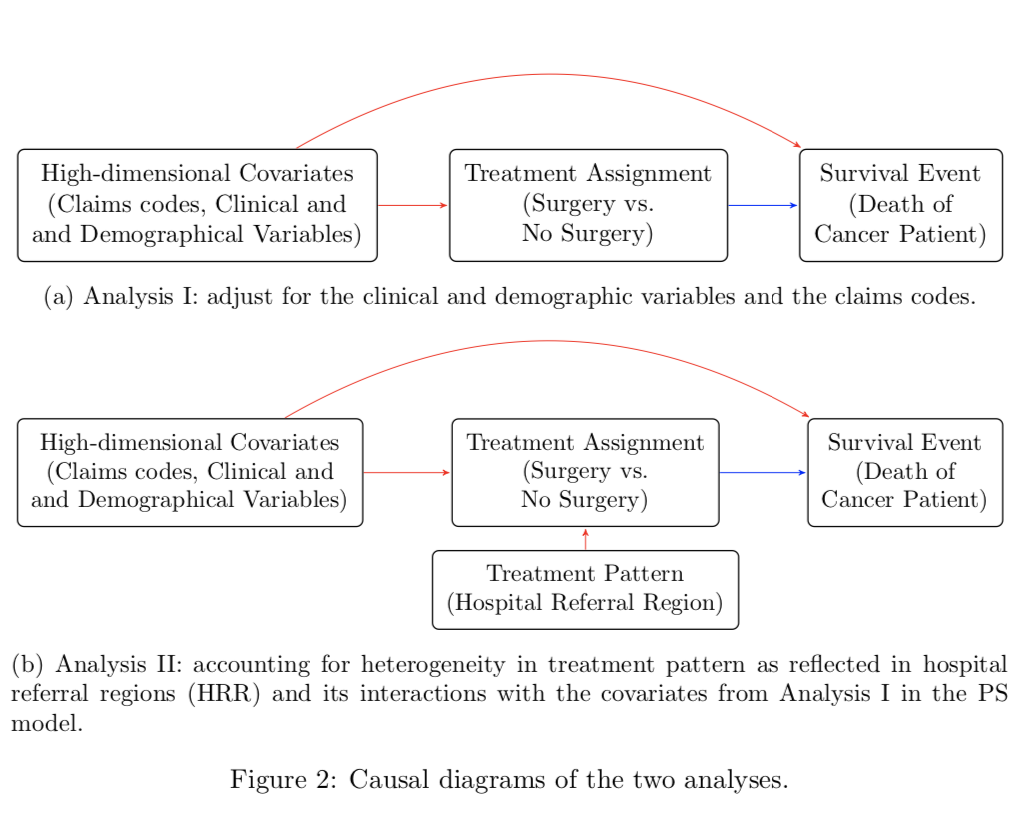
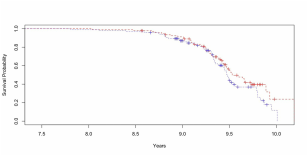
Estimating Treatment Effect under Additive Hazards Models with High-dimensional Covariates

Estimating causal effects for survival outcomes in the high-dimensional setting is an extremely important topic for many biomedical applications as well as areas of social sciences. We propose a new orthogonal score method for treatment effect estimation and inference that results in asymptotically valid confidence intervals assuming only good estimation properties of the hazard outcome model and the conditional probability of treatment. This guarantee allows us to provide valid inference for the conditional treatment effect under the high-dimensional additive hazards model under considerably more generality than existing approaches. In addition, we develop a new Hazards Difference (HDi) estimator. We showcase that our approach has double-robustness properties in high dimensions: with cross-fitting the HDi estimate is consistent under a wide variety of treatment assignment models; the HDi estimate is also consistent when the hazards model is misspecified and instead the true data generating mechanism follows a partially linear additive hazards model. We further develop a novel sparsity doubly robust result, where either the outcome or the treatment model can be a fully dense high-dimensional model. We apply our methods to study the treatment effect of radical prostatectomy versus conservative management for prostate cancer patients using the SEER-Medicare Linked Data.

​      with Jue Hou and Ronghui Xu
          revision at the Journal of the American Statistical Association: T&M

Sparsity Double Robust Inference of Average Treatment Effects

Many popular methods for building confidence intervals on causal effects under high-dimensional confounding require strong “ultra-sparsity” assumptions that may be difficult to validate in practice. To alleviate this difficulty, we here study a new method for average treatment effect estimation that yields asymptotically exact confidence in- tervals assuming that either the conditional response surface or the conditional proba- bility of treatment allows for an ultra-sparse representation (but not necessarily both). This guarantee allows us to provide valid inference for average treatment effect in high dimensions under considerably more generality than available baselines. In addition, we showcase that our results are semi-parametrically efficient.

       with Stefan Wager and Yinchu Zhu
​            submitted

Synthetic Learner:
​model-free inference on treatments over time

Understanding of the effect of a particular treatment or a policy pertains to many areas of interest -- ranging from political economics, marketing to health-care and personalized treatment studies. In this paper, we develop a non-parametric, model-free test for detecting the effects of treatment over time that extends widely used Synthetic Control tests. The test is built on counterfactual predictions arising from many learning algorithms. In the Neyman-Rubin potential outcome framework with possible carry-over effects, we show that the proposed test is asymptotically consistent for stationary, beta mixing processes. We do not assume that class of learners captures the correct model necessarily. We also discuss estimates of the average treatment effect, and we provide regret bounds on the predictive performance. To the best of our knowledge, this is the first set of results that allow for example any Random Forest to be useful for provably valid statistical inference in the Synthetic Control setting. In experiments, we show that our Synthetic Learner is substantially more powerful than classical methods based on Synthetic Control or Difference-in-Differences, especially in the presence of non-linear outcome models.

      with Davide Viviano
​                revision at Journal of Econometrics
​

High-dimensional semi-supervised learning: in search of optimal inference of the mean

We provide a high-dimensional semi-supervised inference framework focused on the mean and variance of the response. Our data are comprised of an extensive set of observations regarding the covariate vectors and a much smaller set of labeled observations where we observe both the response as well as the covariates. We allow the size of the covariates to be much larger than the sample size and impose weak conditions on a statistical form of the data. We provide new estimators of the mean and variance of the response that extend some of the recent results presented in low-dimensional models. In particular, at times we will not necessitate consistent estimation of the functional form of the data. Together with estimation of the population mean and variance, we provide their asymptotic distribution and confidence intervals where we showcase gains in efficiency compared to the sample mean and variance. Our procedure, with minor modifications, is then presented to make important contributions regarding inference about average treatment effects. We also investigate the robustness of estimation and coverage and showcase widespread applicability and generality of the proposed method.

      with Yuqian Zhang
​              revision at Biometrika

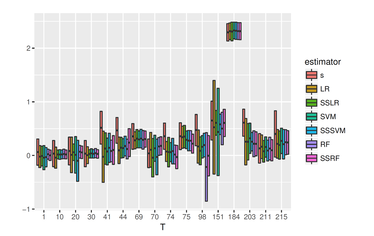
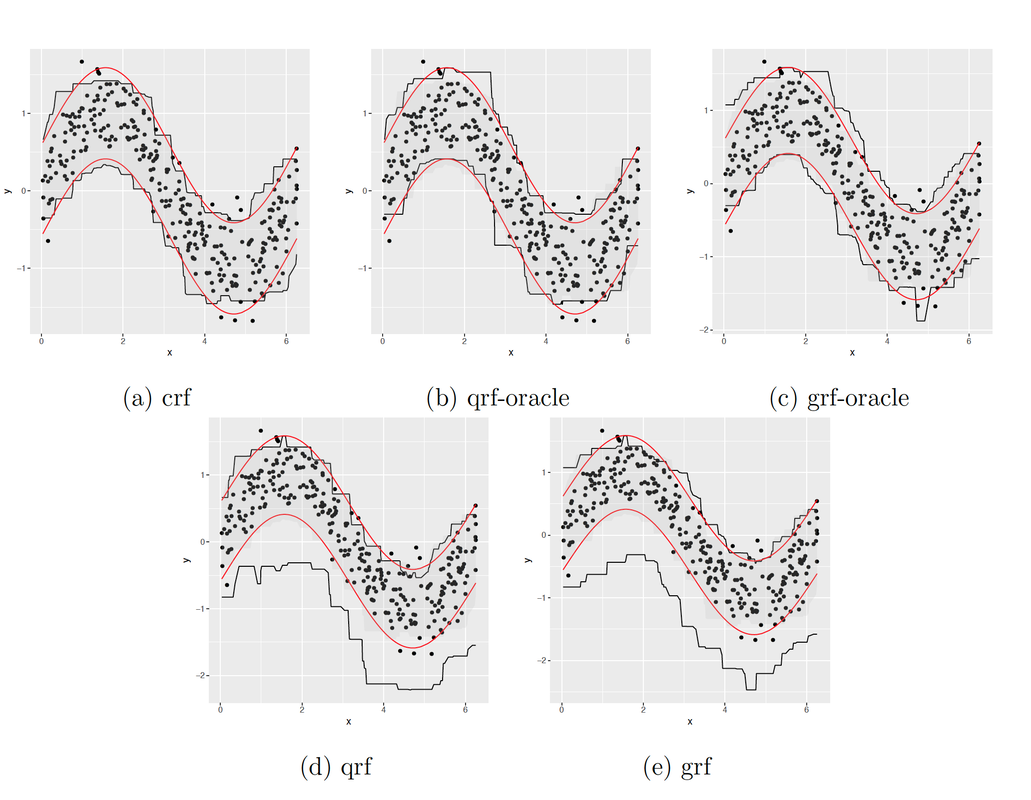
Censored quantile regression forests
Random forests are powerful non-parametric regression method but are severely limited in their usage in the presence of randomly censored observations, and naively applied can exhibit poor predictive performance due to the incurred biases. Based on a local adaptive representation of random forests, we develop its regression adjustment for randomly censored regression quantile models. Regression adjustment is based on new estimating equations that adapt to censoring and lead to quantile score whenever the data do not exhibit censoring. The proposed procedure named {\it censored quantile regression forest}, allows us to estimate quantiles of time-to-event without any parametric modeling assumption. We establish its consistency under mild model specifications. Numerical studies showcase a clear advantage of the proposed procedure.

     with Alexander Hanbo Li
​             AISTATS 2020

Confidence intervals for high-dimensional Cox model

The purpose of this paper is to construct confidence intervals for the regression coefficients in high-dimensional Cox proportional hazards regression models where the number of covariates may be larger than the sample size. Our debiased estimator construction is similar to those in Zhang and Zhang (2014) and van de Geer et al. (2014), but the time-dependent covariates and censored risk sets introduce considerable additional challenges. Our theoretical results, which provide conditions under which our confidence intervals are asymptotically valid, are supported by extensive numerical experiments.
​
     with Richard J. Samworth and Yi Yu
​             to appear at Statistica Sinica

Testability of high-dimensional linear models with non-sparse structures

This paper studies hypothesis testing and confidence interval construction in high-dimensional linear models with possible non-sparse structures. For a given component of the parameter vector, we show that the difficulty of the problem depends on the sparsity of the corresponding row of the precision matrix of the covariates, not the sparsity of the model itself. We develop new concepts of uniform and essentially uniform non-testability that allow the study of limitations of tests across a broad set of alternatives. Uniform non-testability identifies an extensive collection of alternatives such that the power of any test, against any alternative in this group, is asymptotically at most equal to the nominal size, whereas minimaxity shows the existence of one particularly "bad" alternative. Implications of the new constructions include new minimax testability results that in sharp contrast to existing results do not depend on the sparsity of the model parameters. We identify new tradeoffs between testability and feature correlation. In particular, we show that in models with weak feature correlations minimax lower bound can be attained by a confidence interval whose width has the parametric rate regardless of the size of the model sparsity.
​
       with Jianqing Fan and Yinchu Zhu,
​                major revision at AOS

Testing in high-dimensional linear mixed models

Many scientific and engineering challenges -- ranging from pharmacokinetic drug dosage allocation and personalized medicine to marketing mix (4Ps) recommendations -- require an understanding of the unobserved heterogeneity in order to develop the best decision making-processes. In this paper, we develop a hypothesis test and the corresponding p-value for testing for the significance of the homogeneous structure in linear mixed models. A robust matching moment construction is used for creating a test that adapts to the size of the model sparsity. When unobserved heterogeneity at a cluster level is constant, we show that our test is both consistent and unbiased even when the dimension of the model is extremely high. Our theoretical results rely on a new family of adaptive sparse estimators of the fixed effects that do not require consistent estimation of the random effects. Moreover, our inference results do not require consistent model selection. We showcase that moment matching can be extended to nonlinear mixed effects models and to generalized linear mixed effects models. In numerical and real data experiments, we find that the developed method is extremely accurate, that it adapts to the size of the underlying model and is decidedly powerful in the presence of irrelevant covariates.
​
   with Gerda Claeskens and Thomas Gueuning,
​             to appear in the  
​                           Journal of the American Statistical Association: T&M

Fine-Gray competing risks model with high dimensional covariates: estimation and inference

The purpose of this paper is to construct confidence intervals for the regression coefficients in the Fine-Gray model for competing risks data with random censoring, where the number of covariates can be larger than the sample size. Despite strong motivation from biostatistics applications, high-dimensional Fine-Gray model has attracted relatively little attention among the methodological or theoretical literatures. We fill in this blank by proposing first a consistent regularized estimator and then the confidence intervals based on the one-step bias-correcting estimator. We are able to generalize the partial likelihood approach for the Fine-Gray model under random censoring despite many technical difficulties. We lay down a methodological and theoretical framework for the one-step bias-correcting estimator with the partial likelihood, which does not have independent and identically distributed entries. We also handle for our theory the approximation error from the inverse probability weighting (IPW), proposing novel concentration results for time dependent processes. In addition to the theoretical results and algorithms, we present extensive numerical experiments and an application to a study of non-cancer mortality among prostate cancer patients using the linked Medicare-SEER data.
​
    with Ronghui Xu and Jue Hou,
              to appear  at the Electronic Journal of Statistics

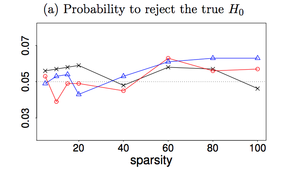
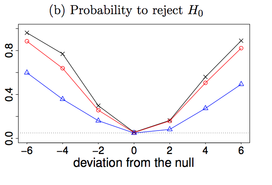
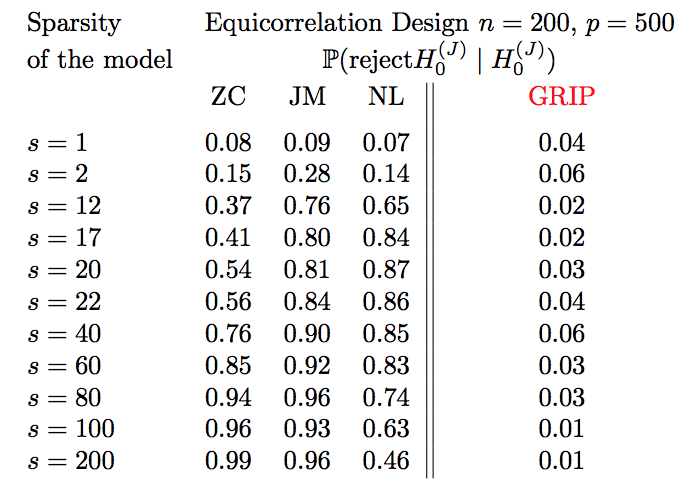
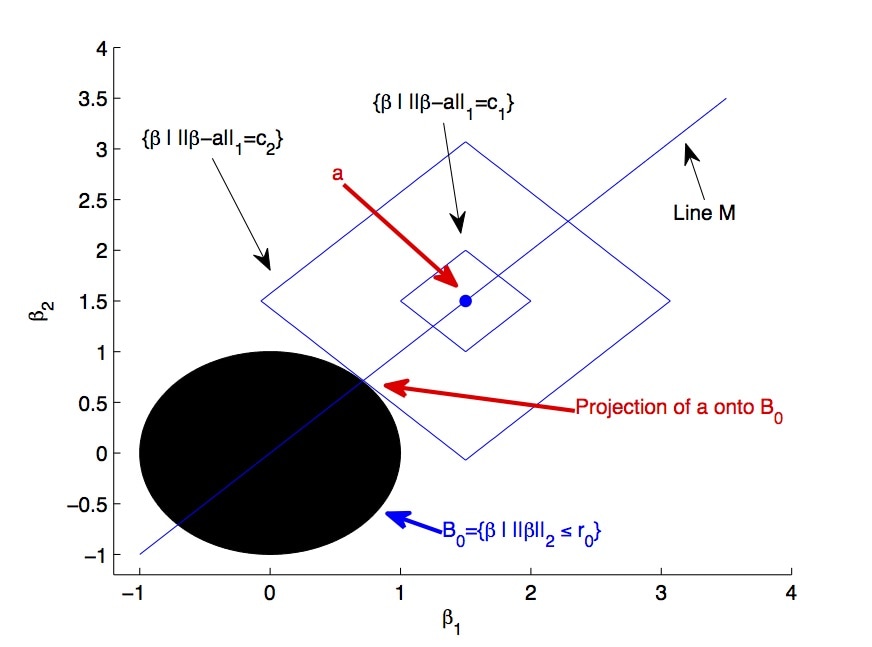
Breaking the curse of dimensionality

Models with many signals, high-dimensional models, often impose structures on the signal strengths.  The common assumption is that only a few signals are strong and most of the signals are zero or close (collectively) to zero. However, such a requirement might not be valid in many real-life applications. In this article, we are interested in conducting large-scale inference in models that might have signals of mixed strengths. The key challenge is that the signals that are not under testing might be collectively non-negligible (although individually small) and cannot be accurately learned. This article develops a new class of tests that arise from a moment matching formulation. A virtue of these moment-matching statistics is their ability to borrow strength across features, adapt to the sparsity size and exert adjustment for testing growing number of hypothesis. GRoup-level Inference of Parameter, GRIP, test harvests effective sparsity structures with hypothesis formulation for an efficient multiple testing procedure. Simulated data showcase that GRIPs error control is far better than the alternative methods. We develop a minimax theory, demonstrating optimality of GRIP for a broad range of models, including those where the model is a mixture of a sparse and high-dimensional dense signals.
​
      with Yinchu Zhu,
           revision requested by the Journal of the Machine Learning Research

​ A projection pursuit framework for testing
         general high-dimensional hypothesis

This article develops a framework for testing general hypothesis in high-dimensional models where the number of variables may far exceed the number of observations. Existing literature has considered less than a handful of hypotheses, such as testing individual coordinates of the model parameter. However, the problem of testing general and complex  hypotheses   remains widely open. We propose a new inference method developed around the hypothesis adaptive  projection pursuit framework, which solves the  testing problems in the most general case.  The proposed inference is centered around a new class of estimators  defined as   $l_1$ projection of  the initial guess of the unknown onto the   space defined by the null.  This  projection automatically takes into account the structure of the null hypothesis and allows us to study formal inference for a number of  long-standing problems. For example, we can directly conduct inference on the sparsity level of the model parameters  and  the   minimum signal strength. This is especially significant given the fact that the former is a fundamental condition underlying most of the theoretical development in high-dimensional statistics, while the latter is a key condition used to establish   variable selection properties. Moreover, the proposed method is asymptotically exact and has satisfactory power properties for testing very general functionals of the high-dimensional parameters. The simulation studies  lend further support to our theoretical claims and additionally show excellent finite-sample size and power properties of the proposed test.
     
​       with Yinchu Zhu,
​               submitted

Comment on "High dimensional
​   simultaneous inference via bootstrap" by Dezeure,                    Buhlmann and Zhang

The authors should be congratulated on their insightful article proposing forms of residual and paired bootstrap methodologies in the context of simultaneous testing in sparse and high- dimensional linear models. We appreciate the clear exposition of their work, and the effectiveness of the proposed method. The authors advocate for the bootstrap of a complete high-dimensional estimate rather than the linearized part of the test statistic. We appreciate the opportunity to comment on several aspects of this article. 
In this comment we discuss residual bootstrap efficiency in high-dimensions, finite-sample performance and correctness and propose a new residual bootstrap sampling that is adaptive to the size of the model sparsity and/or model strength.
​
   with Yinchu Zhu, 
              TEST (2017), 26(4), p.720-728.

 Uniform inference for high-dimensional
      quantile process:
​          linear testing and regression rank scores


Hypothesis tests in models whose dimension far exceeds the sample size can be formulated much like the classical studentized tests only after the initial bias of estimation is removed successfully. The theory of debiased estimators can be developed in the context of quantile regression models for a fixed quantile value. However, it is frequently desirable to formulate tests based on the quantile regression process, as this leads to more robust tests and more stable confidence sets. Additionally, inference in quantile regression requires estimation of the so called sparsity function which depends on the unknown density of the error. In this paper we consider a debiasing approach for the uniform testing problem. We develop high-dimensional regression rank scores and show how to use them to estimate the sparsity function, as well as how to adapt them for inference involving the quantile regression process. Furthermore, we develop a Kolmogorov-Smirnov test in a location-shift high-dimensional models and confidence sets that are uniformly valid for many quantile values. The main technical results are the development of a Bahadur representation of the debiasing estimator that is uniform over a range of quantiles and uniform convergence of the quantile process to the Brownian bridge process, which are of independent interest. Simulation studies illustrate finite sample properties of our procedure.
​
       with Mladen Kolar,
                      Annals of Statistics,  revision

Two-sample testing in non-sparse
                    high-dimensional linear models

In analyzing high-dimensional models, sparsity of the model parameter is a common but often undesirable assumption. In this paper, we study the following two-sample testing problem: given two samples generated by two high-dimensional linear models, we aim to test whether the regression coefficients of the two linear models are identical. We propose a framework named TIERS (short for TestIng Equality of Regression Slopes), which solves the two-sample testing problem without making any assumptions on the sparsity of the regression parameters. TIERS builds a new model by convolving the two samples in such a way that the original hypothesis translates into a new moment condition. A self-normalization construction is then developed to form a moment test. We provide rigorous theory for the developed framework. Under very weak conditions of the feature covariance, we show that the accuracy of the proposed test in controlling Type I errors is robust both to the lack of sparsity in the features and to the heavy tails in the error distribution, even when the sample size is much smaller than the feature dimension. Moreover, we discuss minimax optimality and efficiency properties of the proposed test. Simulation analysis demonstrates excellent finite-sample performance of our test. In deriving the test, we also develop tools that are of independent interest. The test is built upon a novel estimator, called Auto-aDaptive Dantzig Selector (ADDS), which not only automatically chooses an appropriate scale of the error term but also incorporates prior information. To effectively approximate the critical value of the test statistic, we develop a novel high-dimensional plug-in approach that complements the recent advances in Gaussian approximation theory.
​
       with Yinchu Zhu,
​                 submitted

Linear hypothesis testing in dense
​              high-dimensional linear models


Providing asymptotically valid methods for testing general linear functions of the regression parameters in high-dimensional models is extremely challenging -- especially without making restrictive or unverifiable assumptions on the number of non-zero elements, i.e., the model sparsity. In this article, we propose a new methodology that transforms the original hypothesis into a moment condition and demonstrate that valid tests can be created without making any assumptions on the model sparsity. We formulate a restructured regression problem with the new features synthesized according to the null hypothesis directly; further, with the help of such new features, we have designed a valid test for the transformed moment condition. This construction enables us to test the null hypothesis, even if the original model cannot be estimated well. Although the linear tests in high dimensions are by nature very difficult to analyze we establish theoretical guarantees for Type I error control, allowing both the model and the vector representing the hypothesis to be non-sparse. The assumptions that are necessary to establish Type I error guarantees are shown to be weaker than the weakest known assumptions that are necessary to construct confidence intervals in the high-dimensional regression. Our methods are also shown to achieve certain optimality in detecting deviations from the null hypothesis. We demonstrate favorable finite-sample performance of the proposed methods, via both a numerical and a real data example.
​
       with Yinchu Zhu, 
                      Journal of the American Statistical Association: Theory and  Methods, 
                 (2018), 113(524), p. 1583-1600. 
​

High-dimensional inference in linear models:
             robustness and adaptivity to model sparsity


In high-dimensional linear models, the sparsity assumption is typically made, stating that most of the model parameters have value equal to zero. Under the sparsity assumption, estimation and, recently, inference as well as the fundamental limits of detection have been well studied. However, in certain cases, sparsity assumption  may be violated, and a large number of covariates can be expected to be associated with the response, indicating that possibly all, rather just a few, model parameters are different from zero.  A natural example is a genome-wide gene expression profiling, where all genes are believed to affect a common disease marker. We  show that the current inferential methods are  sensitive to the sparsity assumption, and may in turn result in severe bias: lack of control of Type-I error is apparent once the model is not sparse.  In this article, we propose a new inferential method, named CorrT, which is robust and adaptive to the sparsity assumption. CorrT is shown to have Type I error approaching the nominal level, regardless of how sparse or dense the model is.  Specifically, the developed test  is based on a moment condition induced by the hypothesis and the covariate structure of the model design. Such construction circumvents the fundamental difficulty of accurately estimating non-sparse high-dimensional models. As a result, the proposed test guards against large estimation errors caused by potential absence of sparsity, and at the same time, adapts to the model sparsity. In fact, CorrT is also shown to be optimal whenever sparsity holds. Numerical experiments show favorable performance of CorrT  compared to existing methods. We also  apply CorrT to a real dataset  and confirm some known discoveries related to HER2+ cancer patients and the gene-to-gene interaction. 
​
       with Yinchu Zhu,
             Electronic Journal of Statistics, (2018), 12(2), p. 3312-2264.
          

Generalized M-estimators for high-dimensional Tobit I models

This paper  develops   robust  confidence intervals in high-dimensional and left-censored regression.   Type-I censored regression models are extremely  common in practice, where a competing event   makes the variable of interest   unobservable.  However, techniques developed for entirely observed data do not directly apply to the censored observations.  In this paper, we develop smoothed estimating equations   that  augment the   de-biasing method, such that the resulting  estimator  is adaptive to   censoring and is more robust to the misspecification  of the error distribution. We propose a unified class of robust estimators, including Mallow's, Schweppe's and Hill-Ryan's  one-step estimator. In the ultra-high-dimensional setting, where the dimensionality can grow exponentially with the sample size, we show that as long as the preliminary estimator converges faster than n^{-1/4}, the one-step estimator inherits asymptotic distribution of  fully iterated version.  Moreover, we    show   that the size  of the residuals of the Bahadur representation matches those of  the simple linear models, s^{3/4 } (\log (p \vee n))^{3/4} / n^{1/4} -- that is, the effects of censoring asymptotically disappear.  Simulation studies demonstrate that    our method is adaptive to the censoring level  and asymmetry in the error distribution, and does not lose efficiency when the  errors are from symmetric distributions. Finally,  we  apply the developed method to  a real data set from the MAQC-II repository that is related to the  HIV-1 study.
​
​        with Jiaqi Guo,
               Electronic Journal of Statistics, (2019), 13(1), p. 582-645. 

Boosting in the presence of outliers:
​    adaptive classification with non-convex loss functions

 113(512), 660-674, (2018)
This paper examines the role and the efficiency of non-convex loss functions for binary classification problems. In particular, we investigate how to design a simple and effective boosting algorithm that is robust to the outliers in the data. The analysis of the role of a particular non-convex loss for prediction accuracy varies depending on the diminishing tail properties of the gradient of the loss – the ability of the loss to efficiently adapt to the outlying data, the local convex properties of the loss and the proportion of the contaminated data. In order to use these properties efficiently, we propose a new family of non-convex losses named γ-robust losses. Moreover, we present a new boosting framework, Arch Boost, designed for augmenting the existing work such that its corresponding classification algorithm is significantly more adaptable to the unknown data contamination. Along with the Arch Boosting framework, the non-convex losses lead to the new class of boosting algorithms, named Adaptive Robust Boosting (ARB). Furthermore, we present theoretical examples that demonstrate the robustness properties of the proposed algorithms. In particular, we develop a new breakdown point analysis and a new influence function analysis that demonstrate gains in robustness. Moreover, we present new theoretical results, based only on local curvatures, which may be used to establish statistical and optimization properties of the proposed Arch Boosting algorithms with highly non-convex loss functions. Extensive numerical calculations are used to illustrate these theoretical proper- ties and reveal advantages over the existing boosting methods when data exhibits a number of outliers.
​
        with Alexander Hanbo Li,  
           Journal of the American Statistical Association: Theory and  Methods, 
                 (2018), 113(512), p.660-674.

Robustness in sparse linear models:
​   relative efficiency
        and
​           approximate message passing

When the number of parameters p is of the same order as the sample size n, p~n, an efficiency pattern different from the one of Huber was recently established. In this work, we consider the effects of model selection on the estimation efficiency of penalized methods. In particular, we explore whether sparsity, results in new efficiency patterns when p > n.  We propose a novel, robust and sparse approximate message passing algorithm (RAMP), that is adaptive to the error distribution. Our algorithm includes many non-quadratic and non-differentiable loss functions. We derive its asymptotic mean squared error and show its convergence, while allowing p, n, s to converge to infinity, with n/p  is in (0,1) and n/s is in (1,\infty).   We show that the classical information bound is no longer reachable, even for light--tailed error distributions. We show that the penalized least absolute deviation estimator dominates the penalized least square estimator, in cases of heavy--tailed distributions. We observe that the presence of model selection significantly changes the efficiency patterns.
​
        Electronic Journal of Statistics, (2016), 10(2), p. 3894-3944

Randomized Maximum Contrast Selection:
​             subagging for large-scale regression

We introduce a very general method for sparse and large-scale variable selection. The large-scale regression settings is such that both the number of parameters and the number of samples are extremely large. The proposed method is based on careful combination of penalized estimators, each applied to a random projection of the sample space into a low-dimensional space. In one special case that we study in detail, the random projections are divided into non-overlapping blocks; each consisting of only a small portion of the original data. Within each block we select the projection yielding the smallest out-of-sample error. Our random ensemble estimator then aggregates the results according to new maximal-contrast voting scheme to determine the final selected set. Our theoretical results illuminate the effect on performance of increasing the number of non-overlapping blocks. Moreover, we demonstrate that statistical optimality is retained along with the computational speedup. The proposed method achieves minimax rates for approximate recovery over all estimators using the full set of samples. Furthermore, our theoretical results allow the number of subsamples to grow with the subsample size and do not require irrepresentable condition. The estimator is also compared empirically with several other popular high-dimensional estimators via an extensive simulation study, which reveals its excellent finite-sample performance.
       Electronic Journal of Statistics, (2016), 10(1), p. 121-170

Structured Estimation in NonParametric Cox Model

In this paper, we study theoretical properties of the non-parametric Cox proportional hazards model in a high dimensional non-asymptotic setting. We establish the finite sample oracle l2 bounds for a general class of group penalties that allow possible hierarchical and overlapping structures. We approximate the log partial likelihood with a quadratic functional and use truncation arguments to reduce the error. Unlike the existing literature, we exemplify differences between bounded and possibly unbounded non-parametric covariate effects. In particular, we show that bounded effects can lead to prediction bounds similar to the simple linear models, whereas unbounded effects can lead to larger prediction bounds. In both situations we do not assume that the true parameter is necessarily sparse. Lastly, we present new theoretical results for hierarchical and smoothed estimation in the non-parametric Cox model. We provide two examples of the proposed general framework: a Cox model with interactions and an ANOVA type Cox model.
​
       with Rui Song,
          Electronic Journal of Statistics (2015), 9(1), p.492-534

Cultivating Disaster Donors Using Data Analytics

Non-profit organizations use direct-mail marketing to cultivate one-time donors and convert them into recurring contributors. Cultivated donors generate much more revenue than new donors, but also lapse with time, making it important to steadily draw in new cultivations. We propose a new  empirical model   based on importance subsample aggregation of a large number of  penalized logistic regressions. We show via simulation that a simple design strategy based on these insights has potential to improve success rates from 5.4% to 8.1%.
​
       with Ilya Ryzhov and Bin Han,
            Management Science (2016), 62 (3), p. 849-866

Regularization for Cox's proportional
​        hazards model with NP dimensionality

High throughput genetic sequencing arrays with thousands of measurements per sample and a great amount of related censored clinical data have increased demanding need for better measurement specific model selection. In this paper we establish strong oracle properties of nonconcave penalized methods for nonpolynomial (NP) dimensional data with censoring in the framework of Cox's proportional hazards model. A class of folded-concave penalties are employed and both LASSO and SCAD are discussed specifically. We unveil the question under which dimensionality and correlation restrictions can an oracle estimator be constructed and grasped. It is demonstrated that nonconcave penalties lead to significant reduction of the "irrepresentable condition" needed for LASSO model selection consistency. The large deviation result for martingales, bearing interests of its own, is developed for characterizing the strong oracle property. Moreover, the nonconcave regularized estimator, is shown to achieve asymptotically the information bound of the oracle estimator. A coordinate-wise algorithm is developed for finding the grid of solution paths for penalized hazard regression problems, and its performance is evaluated on simulated and gene association study examples.
​
  with Jianging Fan and Jiancheng Jiang,
       The Annals of Statistics (2011) 39(6), p. 3092-3120

Composite Quasi-Likelihood
​       for High Dimensional Variable Selection

In high-dimensional model selection problems, penalized simple least-square approaches have been extensively used. This paper addresses the question of both robustness and efficiency of penalized model selection methods, and proposes a data-driven weighted linear combination of convex loss functions, together with weighted l_1-penalty. It is completely data-adaptive and does not require prior knowledge of the error distribution. In the setting with dimensionality much larger than the sample size, we establish a strong oracle property of the proposed method that possesses both the model selection consistency and estimation efficiency for the true non-zero coefficients. As specific examples, we introduce a robust method of composite L1-L2, and optimal composite quantile method and evaluate their performance in both simulated and real data examples.
​
       with Jianqing Fan and Weiwei Wang,
                       Journal of Royal Statistical Society:
                                              Series B (Statistical  Methodology) (2011), 73(3), p. 325-349